§
57. Способ плоскопараллельного перемещения
Способ
плоскопараллельного перемещения основан на том, что при параллельном переносе
геометрического тела относительно плоскости проекций проекция его на эту плоскость
не меняет своей формы и размеров, хотя и меняет положение. При этом если точка
перемещается в плоскости, параллельной П1, то ее фронтальная
проекция изображается в виде прямой, параллельной оси П2/П1.
Если же точка перемещается в плоскости, параллельной П2, то ее горизонтальная
проекция изображается в виде прямой, параллельной той же оси.
На
рис. 107 показан комплексный чертеж прямой АВ. Прямая не параллельна
ни одной из плоскостей проекций. Требуется с помощью плоскопараллельного перемещения
задать ей такое положение, чтобы она была параллельна одной из плоскостей проекций,
например П2. Через произвольную точку А1, проводим
прямую l1 параллельную оси П2/П1, и
от этой точки на прямой откладываем отрезок, равный
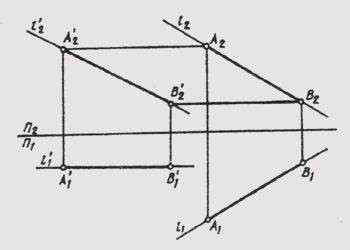
Рис. 107
А1В1.
Из точки А1 проводим вертикальную линию связи, а из точки
AT, — горизонтальную линию, на пересечении которых и будет новое положение
фронтальной проекции А2'. Аналогично проведем вертикальную
линию связи из точки В1 до пересечения с горизонтальной линией,
проведенной из точки B2. Новое положение фронтальной проекции точки
В получим на пересечении этих линий в точке В2'.
После
преобразования чертежа горизонтальная проекция прямой АВ стала параллельна
плоскости П2, а значит, спроецировалась она на эту плоскость в натуральную
величину.
Применяя
метод плоскопараллельного перемещения, можно решать многие задачи, связанные
с определением натуральной величины отрезков, углов, плоских фигур, а также
заданием им нужного положения. Однако он связан с изменением положения геометрической
фигуры в пространстве. В практике же встречаются задачи, при решении которых
при преобразовании комплексного чертежа удобнее оставить положение проецирующего
тела неизменным, а изменить положение плоскостей проекций.