§
47. Расположение плоскости относительно плоскостей проекций. Взаимное расположение
двух плоскостей
По
расположению относительно плоскостей проекций плоскости делят на плоскости общего
и частного положения.
К
плоскостям общего положения относятся плоскости, непараллельные и неперпендикулярные
ни одной из плоскостей проекций. На комплексном чертеже (см. рис. 88) проекции
элементов, которыми задана плоскость, как правило, занимают общее положение.
К
плоскостям частного положения относятся плоскости, параллельные или перпендикулярные
одной из плоскостей проекций.
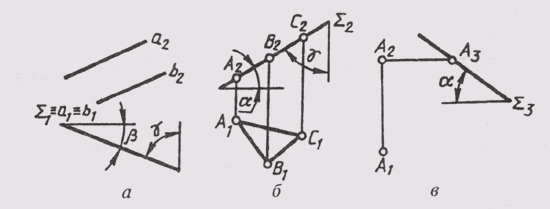
Рис.
89
В
свою очередь, плоскости частного положения делятся на проецирующие плоскости
и плоскости уровня. К проецирующим плоскостям относятся плоскости, перпендикулярные
одной из плоскостей проекций. Все проецирующие плоскости будем обозначать буквой
Е. Проецирующие плоскости могут быть перпендикулярны П1, П2
или П3. В зависимости от этого различают горизонтально проецирующие
плоскости, когда Sum_|_ П1 ; фронтально проецирующие
плоскости, когда Sum_|_П2; профильно проецирующие плоскости,
когда Sum_|_П3;
Проецирующая
плоскость отличается тем, что проекция ее на плоскость проекций, ей перпендикулярную,
всегда изображается в виде прямой линии и фигур, лежащих в проецирующей плоскости.
Проекция плоскости, выраженной в прямой, вполне определяет положение плоскости
относительно плоскостей проекций. Например, на рис. 89, а приведен комплексный
чертеж плоскости I, заданной двумя параллельными прямыми. Из рисунка видно,
что I (а \\ Ъ) является горизонтально проецирующей плоскостью и расположена
под углом Р к фронтальной плоскости проекций и под углом у с фронтальной плоскостью
проекций.
На
рис. 89, б приведен комплексный чертеж плоскости Sum, составляющей угол
а с горизонтальной плоскостью проекций и угол у с фронтальной плоскостью проекций.
Это можно записать так: AВС ~ A2 ~ Sum2,
B2 ~ Sum2, C2 ~ Sum2.
Наличие
вырожденной проекции дает возможность задавать проецирующие плоскости на комплексном
чертеже только одной проекцией. На рис. 89, в через точку А проведена
профильно проецирующая плоскость (Sum_|_П3) под углом а к П1.
Все
изображения, расположенные в заданной плоскости, на плоскости, не перпендикулярные
ей, проецируются с искажением.
К
плоскостям уровня относятся плоскости, параллельные одной из плоскостей проекций.
Их можно считать дважды проецирующими
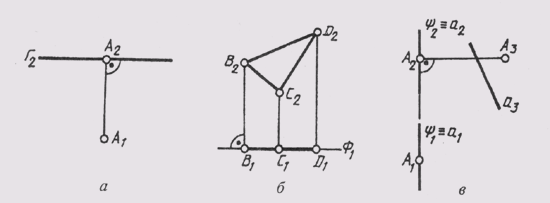
Рис.
90
плоскостями,
так как у них на комплексном чертеже две проекции имеют вид прямой, расположенной
под прямым углом к линии связи, а третья проекция дает изображение всех элементов,
лежащих в этой плоскости, в натуральную величину. Плоскости уровня обычно обозначаются:
Г— горизонтальная плоскость уровня; Ф — фронтальная плоскость уровня;
U — профильная
плоскость
уровня. На рис. 90, а дан комплексный чертеж плоскости горизонтального
уровня (Г || П1); на рис. 90, б приведен комплексный
чертеж плоскости фронтального уровня (Ф || П2), Ф э АВС, А2В2С2
— истинная величина треугольника ABC; на рис. 90, в показан
комплексный чертеж профильно проецирующей плоскости (U || П3, u аА;
А ~ а).
Плоскости
уровня отличаются тем, что на плоскости проекций, им перпендикулярную, они проецируются
в прямую линию, на которой располагаются точки, прямые и фигуры, расположенные
в плоскости уровня. Эти прямые являются вырожденными проекциями заданной плоскости.
На плоскость проекций, параллельную заданной плоскости, все изображения этой
плоскости проецируются без искажений, т. е. в натуральную величину.
Две
плоскости в пространстве могут быть параллельными или пересекаться. Параллельными
будут плоскости, если одна из них задана пересекающимися прямыми, параллельными
пересекающимся, за-
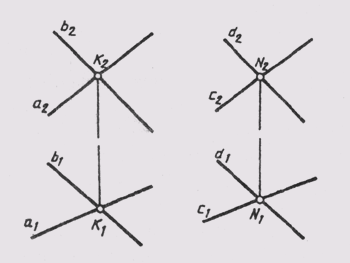
Рис.
91
дающим
вторую плоскость; на рис. 91 показаны параллельные плоскости: Sum (ахb) и
Sum2 (cxd), причем а || с, ab || d.
Если
плоскости пересекаются, то линия их пересечения — прямая. Плоскости, перпендикулярные
между собой, представляют случай их пересечения, когда угол между плоскостями
составляет 90°.
Построение линий пересечения плоскостей рассматривается в §62.