§ 24. Основные элементы геометрического пространства

В инженерной графике геометрическое пространство рассматривается как множество однородных элементов. К основным формообразующим элементам геометрического пространства относятся точки, линии (прямые и кривые), поверхности (плоские и кривые).

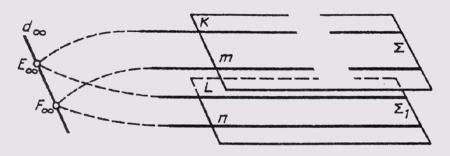
Рис. 42

Различают пространство евклидово и неевклидово. Евклидово пространство характеризуется тем, что расположенные в нем параллельные прямые линии или плоскости не пересекаются. Характеристики евклидова пространства не учитывают ряда других геометрических свойств пространства. В более широком понимании эти свойства учитывают проективное пространство, в котором параллельные между собой прямые (плоскости) пересекаются. Эти пересечения происходят в так называемой несобственной точке, которая расположена в бесконечности проективного пространства. Для примера можно привести две параллельные плоскости S и S₁ (рис. 42). Проведем в плоскости S прямую К, а в плоскости Si прямую L так, чтобы они были параллельны. В проективном пространстве эти прямые пересекаются вне собственной точки Ебесконечность. Далее в плоскости S проведем прямую т, а в плоскости Si прямую п так, чтобы они были параллельны. Эти прямые также пересекутся вне собственной точки F бесконечность. Нетрудно видеть, что несобственные точки Е бесконечность и F бесконечность определяют несобственную прямую d бесконечность . Учитывая, что несобственные точки принадлежат и плоскости S, и плоскости S₁, можно утверждать, что несобственная прямая также принадлежит этим плоскостям. Таким образом, мы имеем случай, когда две параллельные плоскости S и S₁пересекаются по бесконечно удаленной несобственной прямой d бесконечность.

Характеристики проективного пространства позволяют в ряде случаев упростить формулировки, принятые для евклидова пространства. Это можно подтвердить следующим примером. В аксиомах евклидова пространства отмечается, что две прямые определяют единственную точку, если они не параллельны. Для проективного пространства оговорка «если они не параллельны» теряет смысл.

В общепринятом смысле пространство можно рассматривать как бесконечное. Однако геометрическое пространство может быть рассмотрено с позиций размерности. Так, множество положений точки, перемещающейся в заданном прямолинейном направлении, образует бесконечную прямую линию, представляющую собой одномерное пространство. Если же прямую перемещать в заданном направлении, не параллельном самой прямой, она образует бесконечную поверхность (в данном случае плоскость), представляющую собой двухмерное пространство. Задав плоскости (поверхности) направление, не параллельное ей и перемещая ее в этом направлении, получим трехмерное пространство. Таким же путем можно получить четырехмерное и в общем виде многомерное пространство.

Примем следующие обозначения элементов пространства. Точки будем обозначать прописными буквами латинского алфавита: А, В, С... или цифрами 1, 2, 3...; прямые — строчными буквами латинского алфавита: а, b, с..., а плоскости — прописными буквами греческого алфавита: Г, Л, П, S, Ф, ¥, Q.

Между элементами пространства существуют следующие отношения.

Тояадественность обозначается знаком ==, например А == В. Это обозначает, что точка А совпадает с точкой В.

Инцидентность (или принадлежность) обозначается знаком €. Например, А € а обозначает, что точка А принадлежит (инцидентна) прямой а.

Параллельность обозначается знаком ||. Например, K || L обозначает, что прямая К параллельна прямой

Перпендикулярность обозначается знаком _|_. Например, a _|_ S обозначает, что прямая а перпендикулярна плоскости S.

Над элементами пространства можно выполнить операцию соединение, которую обозначают знаком и. Например, запись А и В ~ а обозначает, что в результате соединения точек А и В получена прямая а. Операцию пересечение обозначают знаком ^. Запись т ^ n = К обозначает, что в результате пересечения прямых тип получена точка К.