§
73. Развертки пирамидальных и конических поверхностей
При
развертывании поверхности на плоскости каждой точке поверхности соответствует
единственная точка на развертке: линия поверхности переходит в линию развертки;
длины линий, величины плоских углов и площадей, ограниченных замкнутыми линиями,
остаются неизмеренными. Таким образом, процесс построения развертки сводится
к отыскиванию натуральной (истинной) величины каждого элемента поверхности и
изображению их на плоскости.
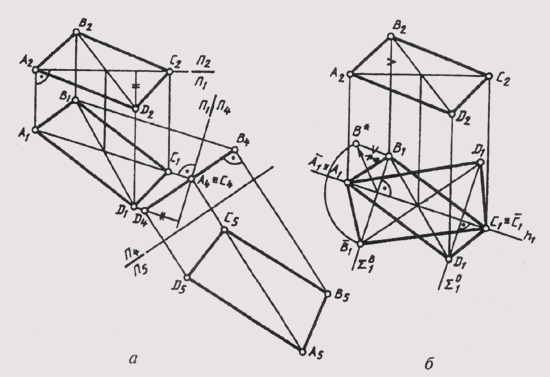
Рис. 146
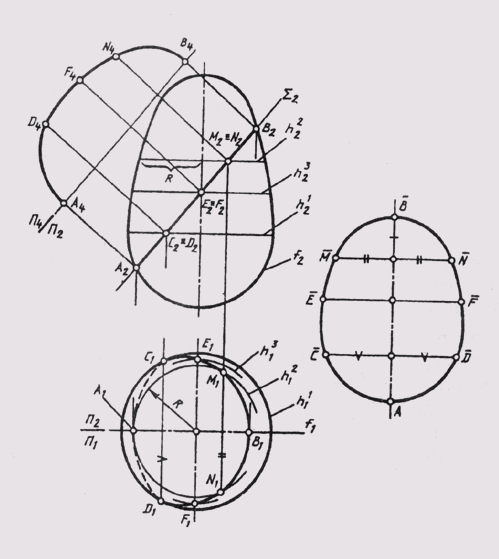
Рис. 147
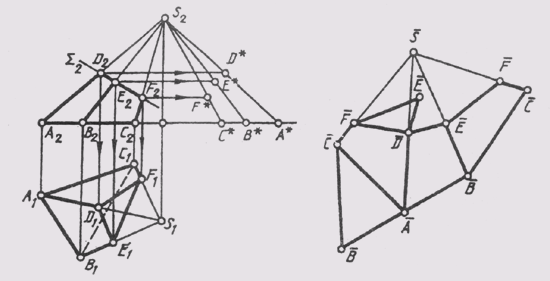
Рис. 148
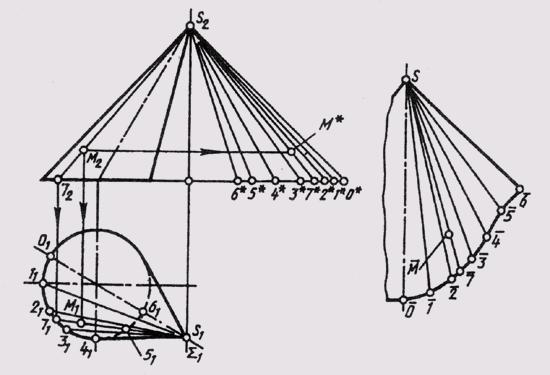
Рис.
149
Каждая
боковая грань на развертке строится как треугольник по трем сторонам. CS
— самое короткое боковое ребро, поэтому рациональнее мысленно разрезать
пирамиду по этому ребру.
Для
нанесения на развертку точек D, Е и F, соответствующих
вершинам сечения пирамиды плоскостью Sum, нужно определить истинные расстояния
этих точек от вершины S. После построения развертки боковой грани поверхности
усеченной части пирамиды нужно пристроить к ней треугольники АBС и
DEF, дающие истинную величину основания и сечения пирамиды.
На
рис. 149 способом триангуляции построена развертка конической поверхности, которая
заменена поверхностью вписанной в нее двенадцатиугольной пирамиды. Развертка
представляет собой симметричную фигуру, так как поверхность имеет плоскость
симметрии Sum. В этой плоскости лежит самая короткая образующая S-6. По
ней и сделан разрез поверхности. Самая длинная образующая S-0 является
осью симметрии развертки поверхности.
Натуральные
величины образующих определены с помощью прямоугольных треугольников, как в
предыдущей задаче на рис. 149. От оси симметрии S-0 строим
шесть в одну сторону и шесть в другую сторону примыкающих друг к другу треугольников
с общей вершиной S. Каждый из треугольников строим по трем сторонам,
при этом две сто-
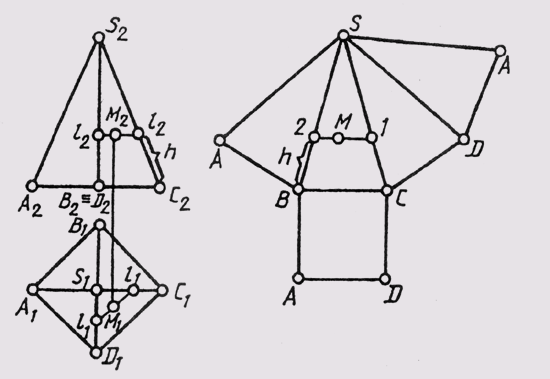
Рис.
150
роны
равны истинным величинам образующих, а третья — хорде, стягивающей дугу окружности
основания между соседними точками деления. Построенные на развертке точки О,
1, 2, ... соединяются. Построение развертки значительно упрощается, если поверхность
представлена прямой пирамидой правильной формы или прямым круговым конусом.
На рис. 150 приведена развертка четырехгранной прямой пирамиды. Построение ее
упрощается тем, что образующая пирамиды AS и CS параллельны фронтальной
плоскости проекций и на нее спроецировались в натуральную величину. Основание
же пирамиды ABCD лежит в плоскости, параллельной горизонтальной плоскости
проекций, и на нее проецируется в натуральную величину. Для построения развертки
достаточно построить сторону AS и сделать засечки радиусом дуги, равным
BS и АВ из точек S и А, соответственно получим точку
В и т. д. Основание же в натуральную величину можно построить на базе
одной из его сторон (на рис. 150 — на базе стороны АВ). Положение точки
на поверхности развертки пирамиды определим в следующем порядке: через фронтальную
проекцию точки М (М2) проведем горизонтальную линию до пересечения
с ребрами A2S2 и B2S2.
Получим точки 11 и 22. На линии AS развертки от точки А отложим
отрезок h и из полученной точки 1 проведем линию 1, 2 параллельно AD
на которой нанесем точку М в том положении, которое она занимает на горизонтальной
проекции линии 1, 2.
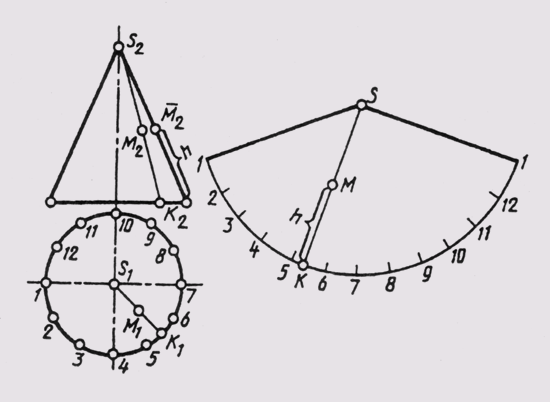
Рис.
151
На рис. 151 приведен пример построения развертки прямого кругового конуса. Для построения ее используем то, что очерковая образующая конуса l на фронтальной плоскости изобразилась в натуральную величину. Выбрав положение вершины развертки — точку S, радиусом L проводим дугу и откладываем на ней 12 равных частей, на которые предварительно разделили окружность основания конуса, изображенного на горизонтальной плоскости проекции в натуральную величину. Чем на большее количество равных участков разделим окружность, тем точнее построим развертку. Положение точки М на развертке поверхности конуса определим следующим образом: через фронтальную проекцию точки проведем образующую и построим горизонтальную ее проекцию. Найдем, что образующая пересекла основание конуса между точками 5 и 6. Точку К переносим на дугу развертки, расположив ее между точками 5 и 6, и соединим с вершиной конуса развертки S. Из точки M2 проведем горизонтальную линию до пересечения с очерковой образующей L и получим точку M2. Расстояние от основания конуса до точки M2 по образующей является высотой точки, которую откладываем на развертке от точки К на линии KS. Полученная точка определит истинное положение точки M на развертке. Таким образом, развертку конической поверхности построим с помощью соседних точек окружности основания, в которую вписан правильный двенадцатиугольник, т. е. коническая поверхность условно заменена поверхностью, вписанной правильной двенадцатиугольной пирамидой, а для построения развертки применен способ триангуляции.