§
61. Пересечение прямой с плоскостью
Прямая
пересекает плоскость в одной точке. Точку пересечения прямой с плоскостью определяют
путем построения вспомогательной прямой линии, лежащей в одной проецирующей
плоскости с заданной прямой. На рис. 119, а приведен комплексный чертеж
прямой l и плоскости 9 (ABC), причем т ~ Q (ABC). Через
горизонтальную проекцию прямой l1 проводим проекцию вспомогательной
горизонтально проецирующей плоскости Sum1. В пересечении плоскостей
Q и Sum получаем линию т, то есть т =Sum ^ Q. Горизонтальная
проекция прямой т определяется горизонтальными проекциями точек 1 и 2
пересечения линий ЕС и АС со вспомогательной плоскостью Sum ,
то есть В1С1 ^ Sum = l1; А1С1
^ Sum1=21; т1 = l1^21.
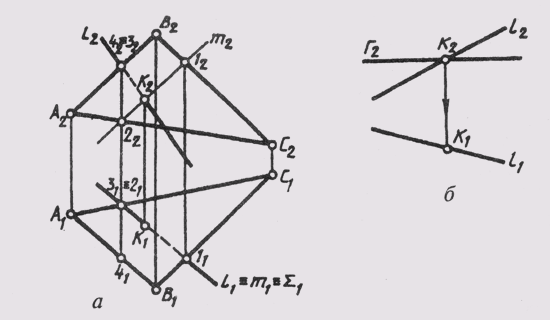
Рис.
119
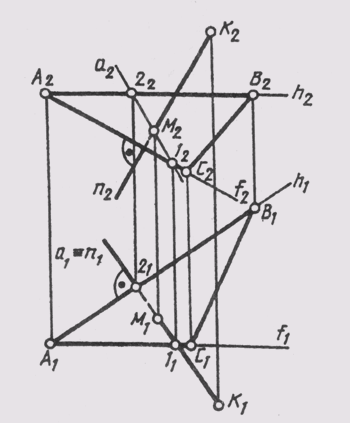
Рис.
120
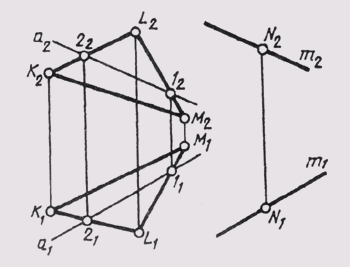
Рис.
121
Для
получения фронтальной проекции линии l построим фронтальные проекции точек 1
и 2, соединив которые, получим фронтальную проекцию m2. В
пересечении фронтальных проекций прямых т и l получим фронтальную проекцию
точки К, принадлежащей и прямой l, и прямой т, лежащей в плоскости
Sum. Значит, точка К и принадлежит плоскости Sum, и является точкой пересечения
прямой l с плоскорью Sum.
Видимость
прямой и плоскости относительно горизонтальной плоскости проекций определяется
с помощью горизонтально конкурирующих точек 2 и 3, а видимость относительно
фронтальной плоскости проекции — с помощью фронтально конкурирующих точек 3
и 4.
Если
плоскость занимает частное положение, то одна проекция точки пересечения прямой
с плоскостью определяется сразу в пересечении вырожденной проекции плоскости
с соответствующей проекцией прямой (рис. 119, б).
Если
прямая пересекает плоскость под прямым углом, то на комплексном чертеже проекции
этой прямой располагаются перпендикулярно проекциям соответствующих линий уровня
плоскости на основании теоремы о проецировании прямого угла (см. § 29).
На
рис. 120 построены проекции основания М перпендикуляра п, проведенного
к плоскости 9 (ABC) из точки К пространства. В AВС имеем:
АВ — горизонталь (A2B2 _|_ A2A1),
AC — фронталь (А1С1 _|_A1A2).
Поэтому проекции перпендикуляра n э К располагаются: п1
_|_A1B1 и n2 _|_ А2С2.
Основание перпендикуляра на плоскости построено с помощью вспомогательной
линии а плоскости, лежащей в одной с перпендикуляром п горизонтально
проецирующей плоскости (а ^ п = М).
Если прямая пересекает плоскость в бесконечности, то имеет место параллельность прямой с плоскостью. На рис. 121 построена прямая т, проходящая через точку N u параллельная плоскости треугольника KLM. На комплексном чертеже параллельность прямой и плоскости доказывается тем, что m1 || а1 и m2 || а2; a ~ KLM.